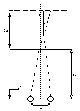
Fig 4: Plan view of the geometrical configuration of an autostereogram.
Fig 4: Plan view of the geometrical configuration of an autostereogram.
For a point with coordinates (x,y,z), rays are drawn directly to the left and right eyes. These rays intersect the plane where the autostereogram lies with x coordinates l and r. So to make an autostereogram, the two points of intersection must hold the same visual information so that both eyes receive identical data, i.e. the points have possess the same colour.
Let s be the point separation so that r = l + s. By the law of
similar triangles [a mathematical law which states that for two triangles
which have the same interior angles, the sides opposite each angle are
related by a fixed ratio], the following relation can be derived
(1)
.
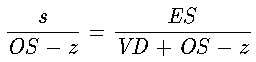This is rewritten as
(2)
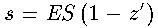
where the new variable z' is defined by
(3)
.
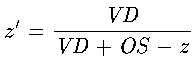Notice that as the point approaches the viewer (as z increases) the
separation s decreases.
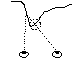Fig 5: Example of a hidden surface.
To make an autostereogram, all of the pixels [picture elements: computer jargon for the small dots that make up a picture on either a monitor screen or some physical media such as paper] (of the final image) must be matched to their stereo partner. The procedure to take is to scan across each line of the image and work out the matching pairs using some depth information. There are several ways to do this; here, only the z-buffer method is explained.
The z-buffer method uses an array to store and check the z values of points within a polygon before applying colour. In making autostereograms, only the depth information is required.
Assuming the buffer is filled with appropriate information --- in this case, the z-buffer is a 2D array with each slot containing the highest z value for a particular (x,y) point on the screen --- it is repeatedly scanned in the x direction, for every y value, and matching points are marked out. Once a horizontal line is traversed, colours are assigned to each pixel in the line subject to the constraints of the matching-pairs list and the line of pixels is drawn on to the screen or written to a file for later use.
There are quite a few methods for implementing this scheme. The simplest way is to ignore the actual geometry and assume that each point lies centrally between your eyes. Then the matching points are given by x +/- s/2. The advantage of this method is the speed of calculation due to its simplicity, but its disadvantage is twofold. Apart from the obvious distortion, the possible circumstance of a surface that is only visible to one eye is ignored. For example, see figure 5. That is, points in a hidden surface would be erroneously included in the matching list.
Nevertheless, for pedagogical reasons some example C code of this scheme is shown. See the next section for more details.
Basically, to incorporate perspective every point in space is projected on
to the plane where the image lies. Again using the law of similar triangles,
a point (x,y,z) is projected to a point (x', y') on the screen where
these new coordinates are related by
(4)
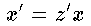and
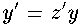
and the variable z' was defined above, in
equation (3).
One way to check for hidden surfaces is to trace the rays back from the eyes and see if they converge to the same point. The disadvantage with this method is that it is slow. A much quicker method stems from the way a z-buffer is used in computer graphics.
With polygonal data for an object, the z-buffer can be filled with z
values of all the points interior to a polygon using linear interpolation
(from the vertex points supplied) because the polygon is planar and obeys
the following equation for a plane
(5)
,
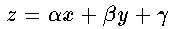where a, b & g are constant for a given polygon.
There is a snag that this does not work for perspective projection, ie.
using (x', y', z). In this case, another function of z is used to fill
the 2D array. A bit of algebra shows that if z' is used and if
equation (5) holds then the following is true
(6)
.
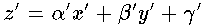This is known as the inverse z-buffer method because z' is a rational
function of z, equation (3).
The inspirational idea to find hidden surfaces is due to Luke Hutchison in private communication with the author. He hit upon the neat idea of using two (instead of one) z-buffers, one for each eye.
His method is to fill each buffer with z values corresponding to the view from each eye then, using the separation function s(z), work out which slot in the right array matches a slot in the left array and compare the z values contained in those slots. If they are the same numerical value (within a given tolerance) then the point represented by the slots is visible to both eyes. As shown in figure 5, a partially hidden point would be seen to possess different z values; the right eye perceives the point having a higher z value than the the left eye does because it is actually seeing a different point.
With the refinement of perspective, this method is much faster than the hidden surface checking mentioned in the Thimbleby paper. The disadvantages include computer memory constraints due to the fact that two large buffers are used, but this can be circumvented by using smaller buffers and processing the image in horizontal strips.
Implementing this method is simple. The only difference is that the
projected x values of each point are different because the eyes are
separated by a horizontal gap. The projected x values are
(7)
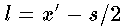and
.
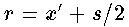Note that since s is a linear function of z', see
equation (2), then equation (6)
still holds when l or r is substituted for x'.
To summarize, for each point (x,y,z) the buffers are filled with the
projected points (l,y',z') and (r,y',z').
Some C code shows the scheme in action.
Ray-tracing is a well-known method of generating realistic computer graphics where, as the name implies, rays are traced from the eye(s) towards the scene, reflecting off objects therein and back to the sources of light. The computer program can be easily changed to trace the rays back to the first object encountered and return with the depth information.
This method is also free from geometrical distortions. Commercial stereograms are generally done with modified ray-tracers.
Most stereogram software available rely on the z-buffer method. In these, the user is required to compose a scene in a variety of methods. Most let the user draw the depth information directly with standard graphics-package tools such as polygonal, elliptical and curved outlines and boundary fills. The depth information is represented as colour, with white as the closest level, black the furthest and greys for intermediate levels. Usually the fills are done with a constant colour though there are exceptions to this that allow gradated fills.
Though this direct approach allows easy manipulation of the scene by the user, the disadvantage is the difficulty of obtaining a realistic 3D scene. Other programs allow the user to handle objects derived from three dimensional data. The problem with this is the limited availability of this data, unless the user has access to a CAD package [Computer Aided Design: used by architects, product designers and engineers to draw 2D and 3D objects and scenes] and/or a large database of pre-designed objects.
Obviously, the ideal program would allow the user to do both these things.
The fact that a computer-generated image will in general consist of
pixels implies that the separation of matching points will be discretized to
units of pixels. This imposes a considerable constraint on the realism of
the depth seen in a stereogram because discrete steps in the separation
means discrete steps in the perceived depth. That is, a layering effect is
seen in the stereogram.
Using the above equations, the number of layers available is
(8)
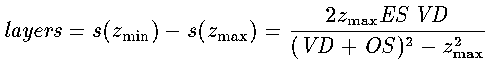
where
.
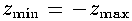Typical values of the parameters are ES = 65*pmm, OS =150*pmm, VD=300*pmm, where pmm (pixels per millimetre) is the pixel resolution of the output device --- a monitor has around 100dpi (dots per inch), which means pmm ~ 4.0.
For a object to fit within the image and appear with the right
proportions, its diameter must be less than the height or width of the
stereogram, whichever is smaller. So for a stereogram of size 1024x768 (in
pixels),
= 384.
Therefore, layers = 77. This
is a low figure though with a greater size (hence a higher resolution --- to
make the stereogram retain a reasonable physical size) it could be much
bigger.
So on a computer screen, stereograms looks noticeably layered. With the higher resolution provided by a laser printer, the printed image is much smoother.
There is a way to reduce the layering effect. This is similar to techniques used to make straight lines in computer graphics appear less jagged.
Briefly, in that situation intermediate colours are used to smooth out the steps. So in coloured stereograms, instead of matching the colour of pixels, the fractional part of the separation value s(z) is used to interpolate the colour between adjacent pixels. This technique works with the side-effect of leaving the resultant image looking a little fuzzy, indicating an effective loss of resolution.