6.1 Weather, butterflies and chaos
Just what is chaos? Perhaps it's best to start with a dictionary definition. The "Oxford Concise
Science Dictionary" defines chaos as: unpredictable and seemingly random behaviour occuring in a system
that is governed by deterministic laws. To understand what that means, we'll briefly consider the work of
Edward Lorenz , an American mathematician who pioneered the study of chaotic systems.
(Note however that Henri Poincare - a famous mathematician who is pictured to the left - first envisaged the possiblity of chaos as early as the turn of the century. Click
here for a short biography.)
It was in attempting to use a computer to determine weather patterns (and thus produce long range weather forecasts) that chaos was first analysed. In 1961 Lorenz set up a weather simulation on a valve-driven computer. He chose a number of simple numerical rules to determine, for example, the relationships between temperature, pressure and wind speed. The system was completely deterministic - Lorenz expected that from the initial conditions he input into his computer model, the precise state of the weather at any future time could be predicted. To examine the patterns of weather simulated by his computer model Lorenz would pick a variable and plot the changes in that variable as a function of time on a chart recorder.
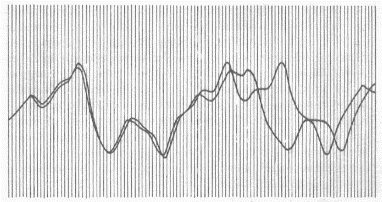Chaos theory originated from Lorenz's serendipitous observation that tiny changes in the initial input conditions
for his weather simulation produced huge differences in the output. The plot to the right ( taken from 'Chaos', James Gleick, p.17 )
shows how the simulated weather patterns for two almost identical starting conditions diverged rapidly until there was no
similarity. This was completely contrary to what Lorenz expected - he likened the small difference in initial conditions to introducing a
tiny puff of wind into his weather system. How could a tiny puff of wind have such a huge influence on the evolution of the weather?
The effect that Lorenz observed has since been termed the butterfly effect . It has been suggested that because the non-linear equations that govern the weather have such an incredible sensitivity to initial conditions, a butterfly flapping its wings in one part of the world may make the difference between a thunderstorm occurring or not occurring in another part of the world!
Non-linearity and an extreme sensitivty to initial conditions are at the heart of chaotic behaviour. However, before we examine some of the properties of chaotic systems, I should stress that chaos cannot override basic laws of physics such as the conservation of energy or the second law of thermodynamics. That is, the incredibly complex patterns of behaviour observed in chaotic systems are subject to the same fundamental constraints as any non-chaotic system.
Move on to Section 6.2: Chaos and the damped, driven pendulum
Home