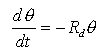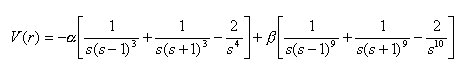Atoms & Molecules at Surfaces : Problems
Modified 12/01/00: I have changed the "Problems" part of the web site so
that the problems may be downloaded as a single file. As I have stated in the lectures on
a number of occasions, I have no plans to add worked solutions to the
problems to the web site, preferring that you hand in your answers to me
so that I can identify and discuss any errors with you.
- For a spherical soap bubble, show that the pressure difference across the soap film is given by:
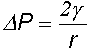
where 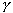 is the surface tension and r is the radius of the bubble.
is the surface tension and r is the radius of the bubble.
- (i)
From the bulk lattice constant of silicon (0.543 nm), taking the Si-Si bond energy as 82 kcal/mol and assuming no surface reconstruction occurs show that of the three low index planes (100), (110) and (111), the Si crystal will naturally cleave to expose the latter surface.
(ii) On cleaving the Si crystal in ultra high vacuum to expose the Si(111) surface, a (2x1) reconstruction is observed with LEED. However, it is known that the Si(111)(7x7) surface has a lower free energy than Si(111)(2x1). Why do you think a (7x7) reconstruction is not observed on cleaving the Si crystal?
(iii) The natural cleavage plane of GaAs (GaAs, like Si, is a tetrahedrally bonded semiconductor) is {110} and not {111}. Can you explain this difference?
- (i)
In addition to the (2x1) structure discussed in the lecture notes, the Si(100) surface is also known to form a c(4x2) reconstruction. Plot the LEED pattern for this reconstruction and sketch possible models of the surface structure consistent with the c(4x2) pattern.
(ii) STM images of the Si(111) surface also show that under certain conditions areas of c(4x2) reconstruction form. Draw the real space basis vectors for this reconstruction and sketch a structural model. (You may assume that the c(4x2) reconstruction is due to Si atoms adsorbed on a bulk-like (111) plane). How is the c(4x2) structure you've drawn related to a Si(111)p(2x2) reconstruction?
- Deposition of 1/3 of a monolayer of group III atoms (Ga, Al, In
etc..) onto the Si(111) surface produces a (
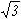 x
x 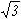 ) R30o reconstruction. Plot the LEED pattern, identifying the integer (bulk) and fractional order diffraction spots. Assuming that the reconstruction is due to metal atoms adsorbed atop an unreconstructed Si(111) surface sketch a structural model consistent with the LEED pattern. Why do you think this reconstruction is observed at a coverage of 1/3 ML of group III atoms? (NB In this case the monolayer unit is defined as a surface coverage equivalent to the surface atom density on an unreconstructed (i.e. bulk-terminated) Si(111) surface).
) R30o reconstruction. Plot the LEED pattern, identifying the integer (bulk) and fractional order diffraction spots. Assuming that the reconstruction is due to metal atoms adsorbed atop an unreconstructed Si(111) surface sketch a structural model consistent with the LEED pattern. Why do you think this reconstruction is observed at a coverage of 1/3 ML of group III atoms? (NB In this case the monolayer unit is defined as a surface coverage equivalent to the surface atom density on an unreconstructed (i.e. bulk-terminated) Si(111) surface).
- Given that we can write the mean relative speed of a molecule in a
gas as vrm=
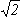 <v>, where <v> is the mean speed of a molecule, show that the mean free path of the molecule is given by Eqn. 3.4 Hint: Assume that a molecule is spherical and moves against a background of molecules that are fixed in position. This is obviously not an accurate description but the use of a mean relative velocity as opposed to a mean velocity enables this simplification to be made. The velocity of the molecule relative to the background molecules is given by Vrm. In order to derive
<v>, where <v> is the mean speed of a molecule, show that the mean free path of the molecule is given by Eqn. 3.4 Hint: Assume that a molecule is spherical and moves against a background of molecules that are fixed in position. This is obviously not an accurate description but the use of a mean relative velocity as opposed to a mean velocity enables this simplification to be made. The velocity of the molecule relative to the background molecules is given by Vrm. In order to derive 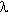 you need to work out the number of collisions the moving molecule makes in unit time. (ii) Show that the mean free path of the molecules in a spherical UHV chamber of 0.5m diameter (P = 1 x 10-10 mbar, T= 300 K) is >> dimensions of the chamber.
you need to work out the number of collisions the moving molecule makes in unit time. (ii) Show that the mean free path of the molecules in a spherical UHV chamber of 0.5m diameter (P = 1 x 10-10 mbar, T= 300 K) is >> dimensions of the chamber.
- C60 or buckminsterfullerene is a perfectly symmetric,
football-shaped molecule consisting of 60 C atoms. Solid C60 (which crystallises in an fcc form with a lattice constant of 1.42 nm) is held at a temperature of 400oC within a Knudsen cell which has an opening of 1 cm diameter and is situated a distance of 5 cm from a Si(111) sample surface. Given that the vapour pressure of C60 at a temperature of 400o C is 1 x 10-5 Torr and that a monolayer of C60 on Si(111) is structurally very similar (assume identical) to the (111) surface of the fcc C60 crystal, calculate the time needed to produce a monolayer of C60 on Si(111). You should assume that every molecule that strikes the Si(111) surface sticks. (NB In this case the monolayer unit is defined as the number of molecules needed to produce a single close-packed layer).
- After baking, a cylindrical UHV chamber (diameter 200 mm, length
350
mm) that is connected to a pump with a pumping speed of 220 ls-1 via a tube of diameter 200 mm and length 100 mm reaches a base pressure of 1x10-10 mbar. Calculate the rate of outgassing from the chamber walls. (Problem 7 adapated from Luth, Chapter 1, Problem 1)
- A very recent study (D. S. Lin and R. P. Chen, Phys. Rev. B
(1999)) has used STM to examine the desorption rate of H from a hydrogen-terminated Si(100) surface. After preparing a Si(100) surface with a 1 ML termination of hydrogen atoms, the surface was annealed at 611 K for a prolonged period of time. The number of sites from which hydrogen desorbed were counted as a function of annealing time and the following results obtained:
|
Coverage of dangling bond sites (ML) * |
Annealing time (s) |
|
0.038 |
2000 |
|
0.065 |
4000 |
|
0.165 |
11000 |
|
0.200 |
13000 |
*
i.e. sites from which hydrogen has been desorbed
(i) Show that these results are consistent with the following simple rate equation:
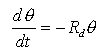
where q is the coverage of desorbing species and Rd is the desorption rate. (Rd = nd exp(-Ed / kT) where nd is the desorption prefactor and Ed is the desorption energy).
(ii) From the data above and given the value of Rd at 668 K, 8 x 10-4 s-1, estimate the desorption energy
- Solid C60 is a molecular crystal. That is, although the C atoms within an individual molecule are held together by strong single and double bonds, the intermolecular forces within the crystal are weak and of predominantly van der Waals character. The Girifalco potential describing the potential for two C60 molecules is:
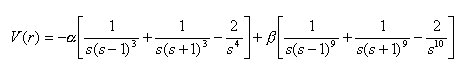
where s=r/d, r is the centre-centre separation of the molecules and d
is
the fullerene cage diameter (0.71 nm). a and
b are constants and equal to 4.68 x 10
-2
eV and 8.43 x 10-5 eV respectively. The potential has a minimum
at r=1.005 nm.
- Estimate the activation energy for diffusion of a single
C60 molecule on the C60 (111) surface
(C60 bulk (fcc) lattice constant = 1.42 nm) [Ans:
Ediff ~ 0.17 eV]. (Consider only one C60(111)
plane)..
How does the activation energy compare with the average energy of thermal fluctuations at room temperature? Is this consistent with the growth of C60 islands on the C60 monolayer at room temperature?
- Determine the ratio of dwell times (at room temperature) for a
C60 molecule bonded in a dimer and in a trimer configuration on
the C60(111) surface. (Use the molecular vibrational frequency
of 1012 Hz).
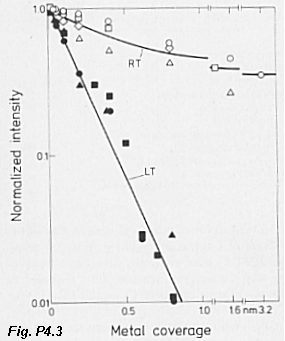
- Fig. P4.3 shows the variation in intensity of the arsenic XPS signal as a function of the amount of Ga evaporated on GaAs(110)(1x1) at both low and room temperature. (Kahn et al. Monch p. 262)
- Explain the differences in the intensity vs coverage curves for room and low temperature;
- Estimate the mean free path of the As core-level electrons in Ga.
- For the low temperature case, sketch how the Ga XPS signal will change as a function of coverage (up to ~ 5nm).
- (i)
We have covered electron depletion layers on n-type semiconductor surfaces. An analogous hole depletion layer can form on a p-type semiconductor surface. What type of surface states, donor or acceptor, need to be present to form a hole depletion layer on a p-type semiconductor? How does charge compensation occur in this case? Sketch a schematic band diagram.
(ii) Photoemission measurements of poorly cleaved p-type (doping
level 1017 cm-3) GaAs(110) surfaces indicate that
the Fermi level is ~ 0.3 eV above the valence band maximum. How thick is
the depletion region? What surface state density does this correspond to?
(Dielectric constant of GaAs = 13.1. Assume that on the ideal,
flatband GaAs surface the Fermi level is degenerate with the
conduction band edge.).
(iii) Why do extended space charge layers not form for metal surfaces?
- a)
Although the currently accepted model for the GaAs(100)(2x4) reconstruction obeys the electron counting rule, the Fermi level at the GaAs(100) surface is found 0.8 ± 0.1 eV above the valence band maximum for both n- and p-type samples. Can you give a reason for this discrepancy?
(b) Deposition of sulphur on an n-type GaAs(100) surface in UHV
with subsequent annealing at ~ 500șC results in the Fermi level moving
closer to the conduction band by 0.5 eV. (i) Sketch schematic band
diagrams before and after sulphur deposition; (ii) Calculate the
surface state density before and after sulphur deposition; (As for
Q.11, assume that the Fermi level is degenerate with the conduction
band edge for the ideal, flatband surface). (iii) A
(2x1) LEED pattern is observed following sulphur deposition and annealing. One proposal is that the (2x1) structure arises from sulphur dimers bonded to a bulk-like Ga-terminated GaAs(100) surface. Is this consistent with electron counting?
- Binnig and Rohrer realised early in the development of the scanning
tunnelling microscope (STM) that, due to the exponential relationship between tip-sample separation and tunnel current, the lateral resolution in STM even with a relatively blunt tip would be much smaller than the true radius of curvature of the tip. They loosely defined an effective radius of curvature for the region of the tip over which the tunnel current fell by ~ an order of magnitude. Show that for a true tip radius of curvature of 100 nm, the effective radius of curvature is ~ 4.5 nm.
- (i) A common method of determining the local barrier height in an
STM
measurement is to modulate the tip height (at a frequency above the feedback loop response rate) and measure the resulting current modulation. Derive, from Eqn. 7.1, the relationship between the quantity measured by this technique and the barrier height.
(ii) The STM operates on the priniciple of tunnelling where the barrier height is greater than the electron energy and thus electron transport over the barrier is classically forbidden. If the barrier height is lower than the electron energy than the barrier is classically allowed and the process is called ballistic transport. Using the uncertainty principle show that for typical electron energies in STM and a barrier width < 0.3 nm, there is no distinction between tunneling and ballistic transport.
- (i) Describe, using band diagrams, how scanning tunnelling spectroscopy may be used to determine the amount of band bending at a semiconductor surface.(ii) Consider an STM investigation of an ideally passivated silicon surface where all the surface states within the band gap have been removed. What effect, if any, does a change in tip-sample separation, at constant bias voltage, have on the band structure of the Si sample? How might you expect this to change for a Si(111)(7x7) sample?
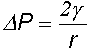
![]() is the surface tension and r is the radius of the bubble.
is the surface tension and r is the radius of the bubble.